Hình 1. Tốc độ tăng trưởng GDP và tỷ lệ thất nghiệp theo quý năm 2011-2023
(Nguồn: Tổng cục Thống kê)
Định luật Okun có thể được biểu diễn bằng công thức sau:
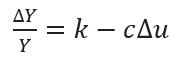
Trong đó: Y là sản lượng thực tế, c là hệ số phản ánh mối quan hệ giữa thay đổi của tỷ lệ thất nghiệp và thay đổi của sản lượng, ΔY là mức thay đổi của sản lượng thực tế, Δu là mức thay đổi của tỷ lệ thất nghiệp thực tế, k là tốc độ tăng trưởng bình quân theo năm của sản lượng toàn dụng. (ΔY/Y chính là tốc độ tăng của sản lượng ).
Định luật Okun là một công cụ hữu ích trong việc đánh giá, dự báo xu hướng giữa tỷ lệ thất nghiệp và sản lượng GDP thực tế. Chúng ta hãy xem xét mối tương quan giữa tăng trưởng hàng quý về GDP thực tế so với những thay đổi hàng quý về tỷ lệ thất nghiệp từ nguồn dữ liệu sẵn có của Tổng cục Thống kê những năm 2011-2023.
Hồi quy thống kê truyền thống
Mục tiêu của mô hình hồi quy tuyến tính truyền thống là tìm ra một phương trình có dạng y = ax + b, trong đó a và b là các hệ số cố định, x là biến độc lập và y là biến phụ thuộc. Phương trình này cho phép dự đoán giá trị của y khi biết giá trị của x, hoặc ngược lại. Định luật Okun thể hiện mối tương quan tuyến tính giữa một biến phụ thuộc là tốc độ tăng GDP và một biến độc lập là mức thay đổi tỷ lệ thất nghiệp (Hình 2).
Hình 2. Mối quan hệ giữa tốc độ tăng GDP và mức độ thay đổi tỷ lệ thất nghiệp
hàng quý năm 2012-2023
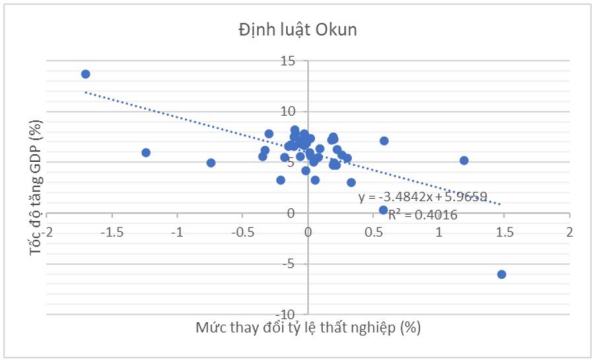
Mô hình hồi quy trên cho biết mối quan hệ thực nghiệm giữa tăng trưởng kinh tế và mức thất nghiệp, theo đó tỷ lệ thất nghiệp theo quý tăng lên 1% khiến tăng trưởng GDP theo quý giảm 3,5%, hay ngược lại, tỷ lệ thất nghiệp giảm 1% khiến tăng trưởng GDP tăng lên 3,5%.
Ở đây hệ số xác định R2 = 0,402. Điều này có nghĩa là mô hình hồi quy tuyến tính của chúng ta giải thích được khoảng 40,2% phương sai của biến phụ thuộc, hay nói cách khác, định luật Okun không phải là một mối quan hệ chặt chẽ, nhưng nó dự đoán rằng sự suy giảm tăng trưởng thường trùng với tỷ lệ thất nghiệp gia tăng.
Chúng ta sẽ sử dụng một số phương pháp hồi quy thống kê hiện đại (Máy học và Bayes) để xem xét lựa chọn mô hình hồi quy nào là thích hợp hơn. Chúng tôi sử dụng tiêu chuẩn R2 để đánh giá hiệu suất và lựa chọn mô hình hồi quy tối ưu. Nếu hệ số xác định có giá trị lớn hơn 50% thì có thể coi mô hình khá phù hợp với tập dữ liệu. Còn nếu hệ số xác định nhỏ hơn 30% thì có thể khẳng định mô hình không phù hợp và nên tìm mô hình khác. Mô hình tốt là một mô hình có khả năng cung cấp các kết quả dự báo càng sát với thực tế càng tốt.
Hồi quy máy học
Hồi quy máy học có thể được coi là một trường hợp riêng biệt của hồi quy thống kê, nhưng với sự tham gia của các thuật toán máy học để tối ưu hóa các tham số của mô hình hồi quy. Chúng tôi sử dụng thư viện Keras để xây dựng mô hình hồi quy. Mạng nơ-ron cho hồi quy là một loại mô hình thống kê sử dụng trọng số thích ứng và có thể xấp xỉ các hàm phi tuyến tính của đầu vào của nó. Nó là một mạng lưới thần kinh được đào tạo, chuyển tiếp và được kết nối đầy đủ có thể được sử dụng để hồi quy, dự đoán và phân loại, bao gồm ba thành phần chính [4].
Lớp đầu vào: Đây là nơi các quan sát huấn luyện được cung cấp. Số lượng biến tiên lượng cũng được chỉ định ở đây thông qua các tế bào thần kinh.
Lớp ẩn: Đây là các lớp trung gian giữa các lớp đầu vào và đầu ra. Mạng nơ-ron sâu tìm hiểu về các mối quan hệ liên quan đến dữ liệu trong thành phần này.
Lớp đầu ra: Đây là lớp mà đầu ra cuối cùng được trích xuất từ những gì đang xảy ra trong hai lớp trước. Trong trường hợp có vấn đề hồi quy, đầu ra sau đó sẽ có một tế bào thần kinh.

Chạy hồi quy Keras ta nhận được kết quả như sau:
Hình 3. Mô hình hồi quy Keras với bộ dữ liệu huấn luyện và kiểm tra
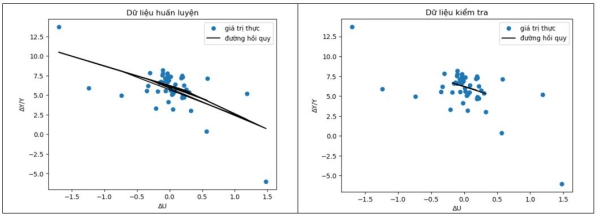
Hệ số xác định R2 của mô hình Keras là 43% lớn hơn hệ số này của mô hình hồi quy thống kê truyền thống là 40,2%. Điều đó cho thấy mô hình hồi quy máy học do được huấn luyện nên phù hợp hơn.
Hệ số hồi quy c = -0,18 cho biết tỷ lệ thất nghiệp tăng lên mỗi 1 điểm phần trăm sẽ dẫn đến tăng trưởng GDP thực giảm 0,18%.
Các mô hình hồi quy thống kê truyền thống hay máy học trên thường được coi là cách tiếp cận thống kê tần suất, là một phương pháp thống kê giúp chúng ta biểu diễn và phân tích dữ liệu theo số lần xuất hiện của các giá trị hoặc nhóm giá trị trong tập dữ liệu. Thống kê tần suất chỉ đơn giản lấy xác suất của một sự kiện nhất định dựa trên các bộ dữ liệu quan sát, kết quả đầu ra là một ước tính điểm, các tham số được xem là không biết luôn không đổi, còn các biến dự đoán là ngẫu nhiên.
Bây giờ chúng ta sẽ tiếp cận mô hình hồi quy theo một cách tiếp cận khác, tiếp cận Bayes, theo đó các yếu tố dự đoán được coi là không đổi trong khi các ước tính tham số là ngẫu nhiên và mỗi tham số tuân theo một phân bố với một giá trị trung bình và phương sai, lúc này kết quả đầu ra không còn là một ước tính điểm đơn lẻ nữa mà là một phân bố.
Hồi quy Bayes
Hồi quy Bayes là một phương pháp hồi quy dựa trên nguyên lý Bayes, trong đó các tham số của mô hình hồi quy được xem như là các biến ngẫu nhiên có phân bố xác suất. Phương pháp này cho phép ta tính toán phân bố hậu nghiệm (posterior) của các tham số dựa trên phân bố tiên nghiệm (prior) và dữ liệu quan sát. Công thức định lý Bayes có dạng:
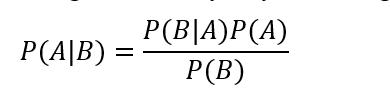
Trong đó:
-
P(A∣B) là xác suất hậu nghiệm của sự kiện A khi biết sự kiện B đã xảy ra.
-
P(B∣A) là xác suất có điều kiện của sự kiện B khi biết sự kiện A đã xảy ra, còn gọi là khả năng của B.
-
P(A) là xác suất tiên nghiệm của sự kiện A, không quan tâm đến sự kiện B.
-
P(B) là xác suất biên của sự kiện B, còn gọi là hằng số chuẩn hóa.
Chúng ta sẽ bắt đầu với hồi quy tuyến tính 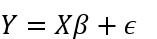
Cú pháp chuẩn cho hồi quy tuyến tính Bayes được đưa ra như sau [2]:
Ở đây, biến kết quả không còn là ước tính điểm nữa mà là phân bố chuẩn với giá trị trung bình của và phương sai , trong đó là phương trình tuyến tính tổng quát trong X.
Mục đích của chúng ta là cập nhật phân bố của các tham số chưa biết β và dựa trên dữ liệu X quan sát được.
Nếu chúng ta coi các thông tin tiên nghiệm của mô hình Bayes là các tham số của mô hình hồi quy tuyến tính truyền thống, ta có các thông tin tiên nghiệm như sau:
Mean Intercept (k): coef: 5.9646 std err: 0.291
Mean slope (c): coef: -3.4863 std err: 0.627
Mean MSE (sigma): 3.888
Tham số hậu nghiệm được ước tính bao gồm các giá trị trung bình thực nghiệm và độ lệch chuẩn của từng biến, cộng với sai số chuẩn của giá trị trung bình.

Đối với mỗi tham số, mcse_mean và mcse_sd là trung bình và sai số chuẩn Monte Carlo, ess_bulk là sai số bình phương trung bình (MSE), ess_tail là hệ số R2 của biến và Rhat là hệ số giảm quy mô tiềm năng trên các chuỗi phân tách (tại độ hội tụ Rhat=1).
Hình 4. Phân bố hậu nghiệm của dự đoán thống kê Bayes
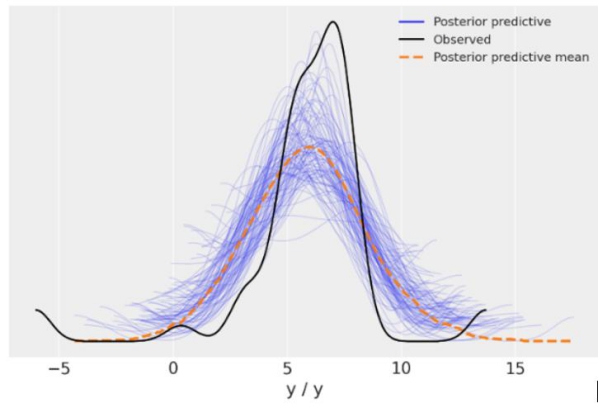
Hình 5. Mô phỏng mô hình hồi quy Bayes
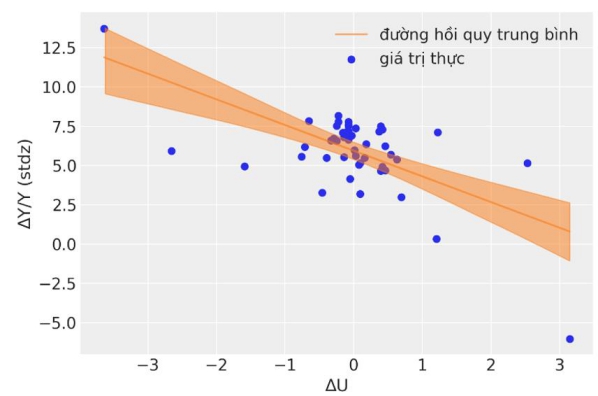
Hệ số R2 của mô hình hồi quy Bayes là 0,402. Điều này có nghĩa là mô hình hồi quy Bayes có khả năng giải thích 40,2% biến động của biến phụ thuộc. Mặc dù mô hình Bayes tính đến sự bất định và biến thiên của các tham số nhưng hệ số xác định này bằng với giá trị R2 của mô hình hồi quy tuyến tính truyền thống. Điều đó cho thấy hai mô hình hồi quy là phù hợp như nhau.
Qua xem xét các mô hình hồi quy thống kê truyền thống, mô hình máy học và mô hình Bayes có thể kết luận rằng mô hình hồi quy Keras máy học là lựa chọn tối ưu (hệ số xác định R2 lớn hơn cả). Định luật Okun trong trường hợp này được viết dưới dạng thức sau:
Định luật Okun cho biết tỷ lệ thất nghiệp theo quý tăng lên 1% khiến tăng trưởng GDP theo quý giảm 0,18%, hay ngược lại, tỷ lệ thất nghiệp giảm 1% khiến tăng trưởng GDP tăng lên 0,18% và được thể hiện bởi hình dưới đây.
Hình 6. Mô phỏng định luật Okun (mô hình Keras)
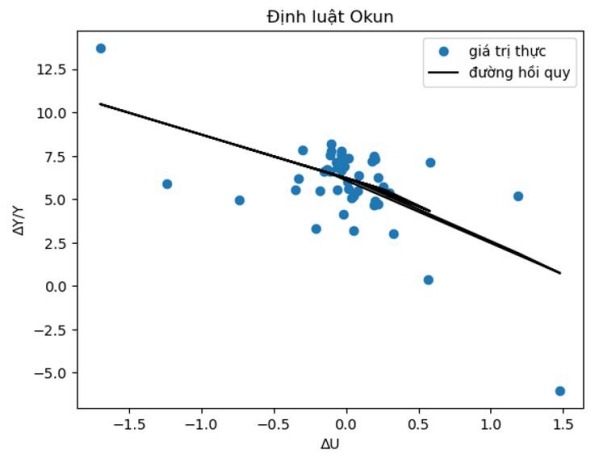
Tuy nhiên, cũng có những tranh luận rằng thực tế mức giảm sản lượng phần lớn do ảnh hưởng của các yếu tố khác bên cạnh tỷ lệ thất nghiệp. Khi giữ cho các yếu tố khác không đổi, với khung thời gian nghiên cứu từ 2011 đến 2023, chúng tôi đã ước lượng sản lượng giảm khoảng 0,18% hàng quý tương ứng với mỗi 1% tăng của tỷ lệ thất nghiệp theo quý.
Như vậy, định luật Okun có ý nghĩa quan trọng trong việc nghiên cứu và dự báo tình hình tiền lương và thất nghiệp trong một nền kinh tế. Nó cũng được sử dụng để đánh giá hiệu quả của chính sách kinh tế và các biện pháp hỗ trợ thị trường lao động. Các kết luận rút ra từ định luật Okun có thể chấp nhận được ở một chừng mực nhất định và là một công cụ phân tích xu hướng ngắn hạn hơn là cho các phân tích dài hạn hay các tính toán đòi hỏi sự chính xác.
Đồng thời chúng tôi muốn khẳng định rằng việc sử dụng các phương pháp thống kê hiện đại đã giúp phát hiện các mối quan hệ và xu hướng trong dữ liệu, suy luận, dự đoán và ra quyết định dựa trên các số liệu thống kê và các mô hình toán học một cách khoa học và chính xác hơn trong nhiều lĩnh vực khác nhau./.
Tài liệu tham khảo
-
Định luật Okun - Wikiwand
-
GLM: Linear regression — PyMC 5.10.3 documentation
-
Okun’s Law: Economic Growth and Unemployment (investopedia.com)
-
Tensorflow & Keras Tutorial: Linear Regression (learnopencv.com)
TS. Phạm Đăng Quyết
Hội Thống kê Việt Nam